En mi caso como principiante para entender de forma básica los números complejos, empezaría por relacionar los números imaginarios con algo conocido, SIN MATEMÁTICAS, explicado para no matemáticos.
Empieza por hallarles relación a los números imaginarios y los números negativos ¿Sabes contar números negativos? ¿que tienen que ver números negativos con los imaginarios y los complejos?
Pues sigue este tutorial paso por paso que no hay información de relleno, si te saltas algo no entenderás lo que sigue.
Iniciamos por dibujar una recta numérica que incluya el rango del -5 al 5
Pregunta, ¿son iguales los números negativos que los números positivos? Respuesta NO, por ejemplo cuando el panadero te dice que cuesta la pieza $4 pesos el espera que le des $4 pesos constantes y sonantes, no le vas a decir “pues tengo $4 pesos negativos o sea que te los pago a fin de año” si no acostumbra a fiar el panadero le parecerá un chiste de mal gusto y te va a decir, “tienes o no tienes dinero, si tienes $4 negativos no te puedes llevar nada, cuando tengas $4 pesos positivos te lo llevas y no me hagas perder tiempo”
El anterior ejemplo ilustra que no es lo mismo números negativos que positivos, pero ¿tienen algo en común los números negativos y los números positivos? Respuesta SI, ¿entonces que tienen en común? ¿que no me acabas de decir que son diferentes? Si son diferentes pero comparten algo en común por ejemplo.
Por ejemplo en un partido de futbol que tienen en común los que le van al equipo azul y los que le van al equipo amarillo, “tienen en común que forman parte del conjunto de personas reunidas en el estadio, pero cada persona reunida es diferente”.
“El Chompiras” y “El Botija” viven en el mismo edificio, pero “tienen en común que forman parte del conjunto de personas que viven donde mismo, pero cada persona es diferente”.
En un zoológico hay un León y un Chimpancé, pero aunque diferentes pero “tienen en común que forman parte del conjunto de animales del mismo zoológico”.
EL SIGUIENTE EJEMPLO ES EL BROCHE DE ORO
En un conjunto musical puede haber un baterista, un guitarrista y un pianista, pero cada músico es diferente, “tienen en común que forman parte del conjunto musical”
De la misma manera al igual que los números negativos y positivos viven dentro de la misma habitación, si los números negativos y positivos forman parte de un conjunto más grande llamado “CONJUNTO DE LOS NÚMEROS REALES”
¿Que hay en el conjunto de los números reales? ¿quienes son los inquilinos del conjunto de los números reales?
Respuesta correcta: Dentro del conjunto de los números reales están
- Los números negativos ejemplo -44, -8, -9
- Los números positivos 5, 89, 23
- Los números enteros
- Los números racionales .25, .75, -64, -21
- Los números irracionales, ejemplo el número Pi, o la raíz cuadrada de 1.5 TODA LA LISTA ANTERIOR ENGLOBA LOS NÚMEROS REALES, LLAMADO CONJUNTO DE LOS NÚMEROS REALES
Pero los números reales tienen de vecino a unos números llamados NÚMEROS IMAGINARIOS, esto significa que tanto “el conjunto de los números reales” y “el conjunto de los números imaginarios” forman parte de algo mucho más grande llamado “CONJUNTO DE LOS NÚMEROS COMPLEJOS”
Es como decir que nuestro planeta tierra y la luna forman parte de algo más grande el sistema solar
Es como decir que los números Reales y los Números imaginarios forman parte de algo más grande, los números complejos.
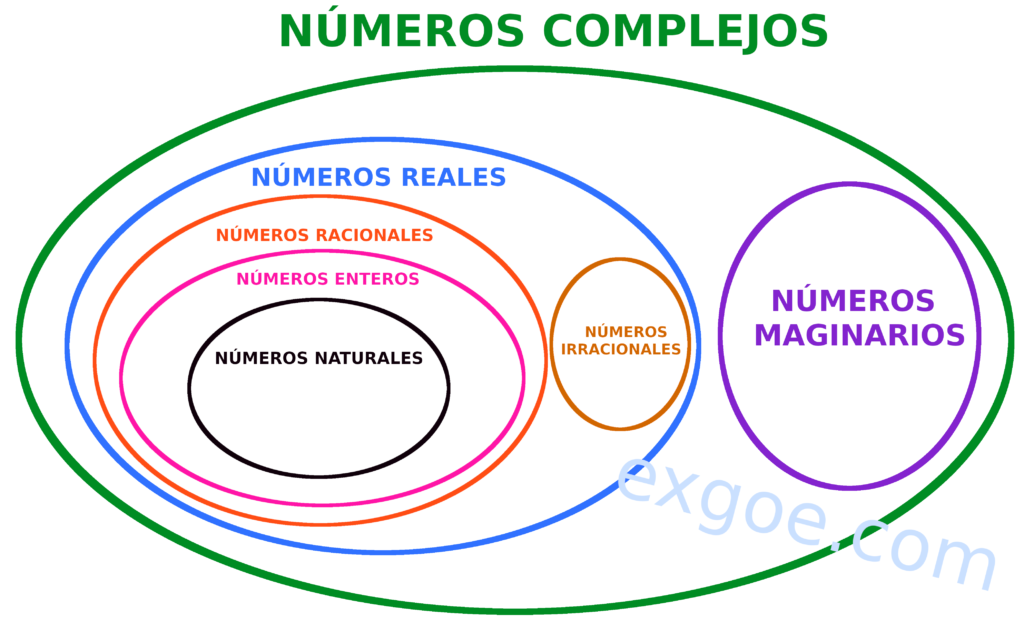
Vea por favor la siguiente imagen que ilustra lo anterior
¿Y que tiene que ver la recta numérica anterior? Pues dejame decirte que los números imaginarios allí están escondidos, pero ahora mismo te los enseñare en la recta numérica.
Entonces la suma de un número Imaginario y de un número real da como resultado un número complejo, lo que ves en la grafica es la representación de números complejos.
Por último como plus para tus clases de números complejos de dejo el siguiente cuadrante, ese no te lo voy a explicar, pero en tus primeras clases de números complejos e imaginarios estoy seguro que te será de mucha ayuda.
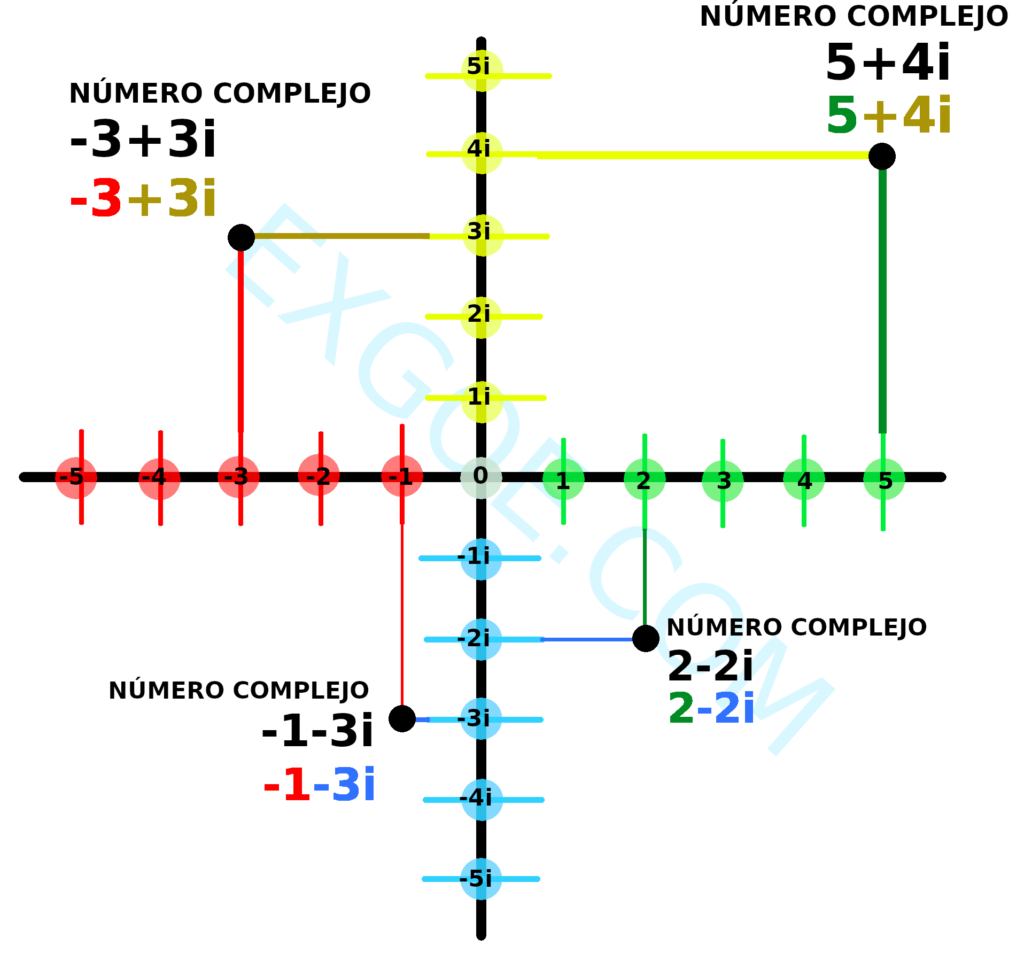
Representación pictórica de los números complejos, reales e imaginarios
Explicando la anterior imagen con detalle
Los números verdes son números POSITIVOS REALES
Los números rojos son números NEGATIVOS REALES
Los números amarillos son números IMAGINARIOS POSITIVOS
Los números azules son números IMAGINARIOS NEGATIVOS
El número 5+4i es un número COMPLEJO porque el número 5 es real positivo y el número 4i es imaginario positivo(dicho en coloquial inexacto será como la intersección de la calle 5 intersección con 4i)
El número 2-2i es un número COMPLEJO con un número real positivo y un número imaginario negativo
El número -1-3i es un número COMPLEJO con un número real negativo y un número imaginario negativo
El número -3+3i es un número COMPLEJO con un número real negativo y un número imaginario positivo
siguiente entrada habla de como convertir un número complejo en forma polar en este link
1 comment